Exemple générique 2.
Polynômes de degré 3.
1- Montrer que $f$ est dérivable sur $\mathbb{R}$ et donner ci-dessous l'expression algébrique de $f'$. Pour tout $x$, $f'(x)=$
2-a/ Chercher le signe de $f'$ en suivant le protocole de recherche ci-dessous: $f'$ est du type $ax^2+bx+c$ , avec $a=$ , qui est donc non nul. Il s'agit donc d'un trinôme du second degré, et pour en trouver le signe, on cherche au préalable ses racines éventuelles: Son discriminant $\Delta$ est de: Comme $\Delta$ est , le trinôme admet dès lors:
Cette racine est de $x_0=$
La plus petite des racines est $x_1=$ et la plus grande est$x_2=$
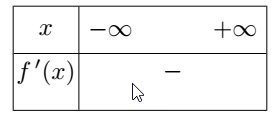
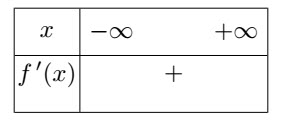
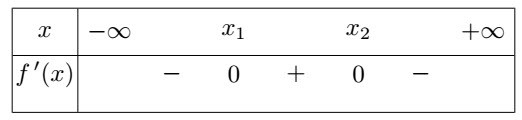
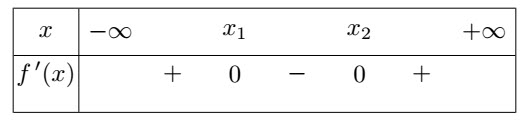
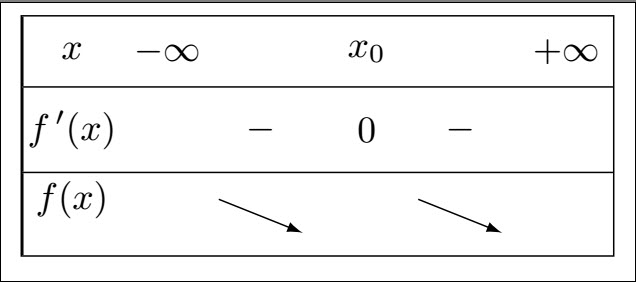
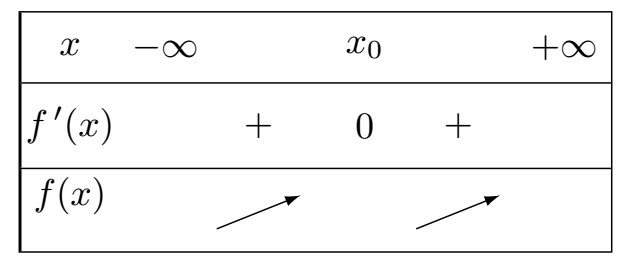
2-b/ Préciser parmi les tableaux suivants, le n° de celui donnant le signe de $f'$ en fonction de $x$
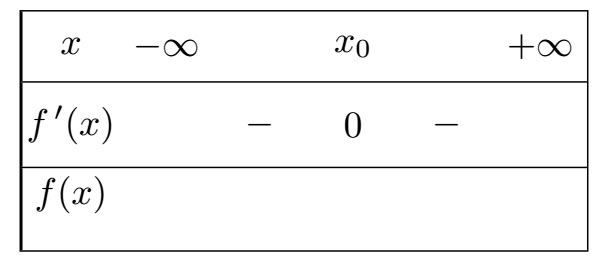
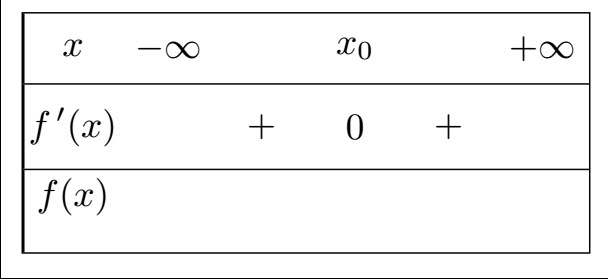
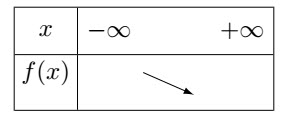
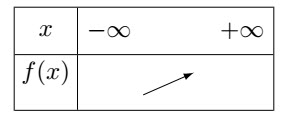
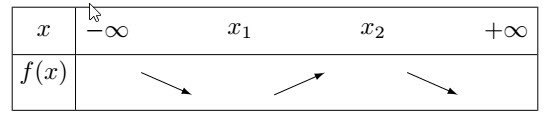
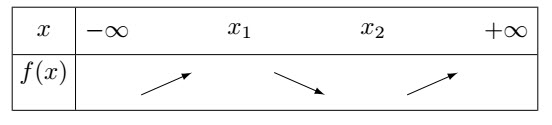
2-c/ Préciser parmi les tableaux suivants, le n° de celui précisant la variation de la fontion $f$
