2.
Attention, votre navigateur ne supporte pas le javascript ou celui-ci a été désactivé. Certaines fonctionnalités dynamiques de ce module sont restreintes.
Préciser le nombre de sous-ensembles d'un ensemble à 6 éléments.
On peut par exemple dénombrer dans l'ordre, les parties à 0,1,2...6 éléments. On rappelle qu'en tant qu'ensembles,
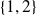et
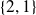désignent le même objet !
On rappelle que l'univers est formé de ses issues, et que l'ensemble des parties de l'univers est formé de ses événements. Dans un ensemble fini de cardinal
, il y a
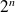événements : un ensemble à n éléments comporte
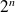sous-ensembles :
En effet, disons que
.
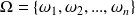Choisir un sous-ensemble de
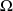revient à interroger chacun des
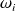énumérés précédemment et lui demander s'il est non dans ce sous-ensemble. Il répondra 1 s'il y est, et 0 sinon. Ceci jette une correspondance biunivoque entre l'ensemble des parties de l'univers et l'ensemble des mots à n lettres formés des seules lettres 0 et 1.
Or, sur un tel nombre binaire à n chiffres caractéristiques, on à 2 possibilités pour le premier chiffre, 2 possibilités pour le second chiffre, etc.
On obtient bien les
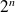possibilités espérées.
Exemple de mise en œuvre du protocole ci-dessus sur un univers à trois éléments :
Soit
Les sous-ensembles de
sont :
, événements que la procédure ci-dessus associe respectivement aux nombres binaires 000,100, 010, 001, 110, 101, 011, 111.
