3
Un hôpital comporte deux salles d'opérations (notées S1, S2) qui ont la même probabilité d'être occupées. La probabilité que I'une des salles au moins soit occupée est 0, 9.
La probabilité que les deux salles soient occupées est 0, 5.
Question
Dans cet exercice, explicite l'univers de probabilité, et les événements considérés dans cet exercice.
Le plus difficile est de cerner l'expérience aléatoire réalisée, et l'univers qui nous intéresse.
Ici, à un moment donné, on s'intéresse à l'occupation des deux salles de l'hôpital: on notera
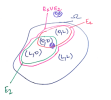
(L, L) l'issue “les deux salles sont libres”,
(L, 0) l'issue “la première salle est libre et la seconde occupée”, qui est différente de (O, L)
et (O, O) l'issue “les deux salles sont occupées”.
Et l'univers est donc formé de ces quatre issues.
Appelons E1 l’événement “S1 est occupée”, et E2 celui “S2 est occupé” :