4. (difficile)
Théorème d'inclusion-exclusion.
Soit
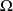un univers fini et
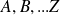des événements quelconques de l'univers.
Pour
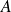donné, on appelle fonction caractéristique de
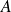, la fonction de
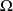dans
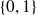prenant la valeur 1 sur
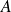et 0 ailleurs : elle sera notée
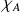. (on la dénomme également fonction indicatrice de
)
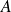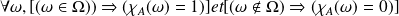
On jette ainsi une correspondance biunivoque entre l'ensemble des parties de l'univers et l'ensemble des fonctions de
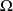dans
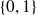: on peut construire la correspondance réciproque qui à une fonction de
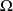dans
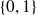associe la partie de
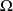constituée des antécédents de 1.
On va dès lors parvenir à relooker les opérations d'union et d'intersection d'ensembles avec un habillage numérique d'opérations sur les fonctions.
Démontrer que
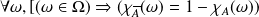]Si on appelle
la fonction
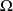constamment égale à 1, (ie : la fonction caractéristique de l'univers), l'égalité précédente étant vraie pour tout élément
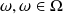, on peut écrire en terme d'égalités de fonction que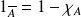
Démontrer que les fonctions
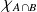et
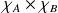sont égales :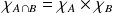
En écrivant de manières différentes
( barbare ?), démontrer que :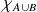
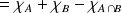
Vérifier que pour tout événement
,
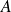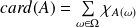
Déduire des questions précédentes que:
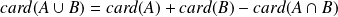
En raisonnant de la même manière, écrire une formule analogue pour
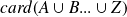( théorème d'Euler-Poincaré, dit d'inclusion-exclusion)
