Introduction
Une histoire d'urne.
Voici un exemple simple: Une urne opaque, que l'on a mélangée consciencieusement, contient huit boules indiscernables au toucher, 5 rouges, et le reste noir. On tire une boule au hasard, et on s'intéresse à sa couleur.
L'expérience menée ci-dessus dépend du hasard. Les issues possibles et appréhensibles de l'expérience primaire réalisée sont constituées des 8 événements élémentaires \(B_1, B_2, B_3, B_4, B_5, B_6, B_7\) ou \(B_8\): l'une quelconque de ces huit boules, certes discriminées par leur couleur, est amenée à être tirée au hasard!
Ici, on s'intéresse moins à la boule elle-même qu'à sa couleur, ce qui s'apparente en fait à une modification de l'univers initial:
Si l'on applique par exemple le filtre de la couleur, les seules issues sont alors \(\lbrace noir, rouge \rbrace.\)
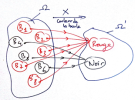
Au départ, notre univers est \( \Omega= \lbrace B_1, B_2...B_8 \rbrace.\)
Cet univers fini est implicitement par l'énoncé, muni de la loi d'équiprobabilité: chacune des issues a la même probabilité de 1/8.
On fait agir la fonction \(X : \Omega → \lbrace noir, rouge \rbrace\), qui associe une boule à sa couleur. (Ici, dans ce contexte probabiliste, la fonction se notera \(X\) et non \(f\) comme usuellement en analyse ). Cette fonction nous permet de nous intéresser à ce qui nous intéresse dans cette expérience aléatoire, non pas les boules en elles-même, mais leur couleur.
Par le biais de cette fonction, la probabilité \(p\) définie initialement sur \(\Omega \) se déverse sur \(\Omega '= \lbrace noir, rouge \rbrace\)
Et on peut ainsi définir les issues \(“noir”\) et \(“rouge”\) et leur probabilité associée, que l'on écrira par exemple \(p(X=”rouge”)\), et qui sera la probabilité sur \(\Omega\) de l'événement constitué des boules rouges. Dans l'exemple présent cette probabilité est de ⅝.
Cette fonction \(X\) qui agit sur l'univers est appelée variable aléatoire. Comme l'univers de départ est fini non vide, la théorie en est grandement simplifiée...Une variable aléatoire est simplement une fonction de l'univers vers un autre ensemble non vide. On s'intéressera aux valeurs images par \(X\). Comme elles sont en nombre fini, on parlera de variable aléatoire discrète.