Loi de probabilité d'une variable aléatoire.
“Alea jacta est.”
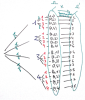
On jette deux fois successivement un dé tétraédrique équilibré, et on s'intéresse à la somme des numéros obtenus: Les résultats de cette expérience aléatoire sont les couples \((1,1), (1,2), ..., (1,4), ... (4,1) ... (4,4)\). Soit 16 issues qui constituent l'univers \(\Omega\) régi par l'équiprobabilité. A chacune de ces issues, on associe la somme des numéros: à chacun des couples \((a,b)\) de l'univers on associe le nombre somme des numéros \(a+b\). Ce qui est visualisé sur l'arbre des possibles ci-dessous.
Appelons \(X\) la fonction somme des numéros qui transforme l'univers \(\Omega\) en \(\Omega ‘\):\( X : \Omega →\Omega ‘\) Chacune des issues de \(\Omega\) est équiprobable, ce n'est pas le cas dans\( \Omega ‘\), qui est constitué des nombres de 2 à 8 images des couples de \(\Omega\) par la variable aléatoire \(X\) :
Précisons la loi de probabilité de \(X\), c'est à dire chacune des probabilités des événements élémentaires de \(\Omega ‘\): La probabilité que \(X\) prenne la valeur 2, que l'on écrira \(p(X=2)\), est la probabilité de l'événement {(1,1)} de \(Ω\): soit 1/16: on écrira donc: \(p(X=2) = 1/16\). La probabilité que \(X\) prenne la valeur 3, que l'on écrira \(p(X=3)\), est la probabilité de l'événement {(1,2), (2,1)} de \(\Omega\) : soit 2/16: on écrira donc: \(p(X=3) = 2/16\)...
Ainsi, l'énumération de toutes les valeurs prises par \(X\) et la donnée de toutes les probabilités associées s'appellera la loi de probabilité de \(X\), et caractérise au mieux l'action probabiliste de la fonction \(X\).
Valeurs \(x_i\)prises par \(X\) | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
Probabilités associées : \(P(X=x_i )\) | 1/16 | 2/16 | 3/16 | 4/16 | 3/16 | 2/16 | 1/16 |
La connaissance des valeurs prises par la fonction X, et de leurs probabilités atomiques, la loi de probabilité de la variable aléatoire X donc, suffit à la description probabiliste de l'action de X: On a même plus besoin alors de se référer à l'univers initial et à la probabilité qui le régit.