Intervalles de fluctuation au seuil de 95 %
Exemple : L'affaire Castaneda VS Partida
En Novembre 1976 dans un comté du sud du Texas, Rodrigo Partida était condamné à huit ans de prison.
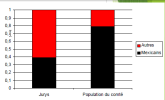
Il attaqua ce jugement au motif que la désignation des jurés de ce comté était discriminante à l'égard des Américains d'origine mexicaine. Alors que 79,1% de la population de comté était d'origine mexicaine, sur les 870 personnes convoquées pour être jurés lors d'une certaine période de référence, il n'y eût que 339 personnes d'origine mexicaine.
Lors du procès, un statisticien produisit des arguments pour convaincre la Cour Suprême du bien fondé de la requête de l'accusé (dont les juges votèrent à 5 contre 4 en faveur de la requête).
Il expliqua que le hasard ne peut pas « raisonnablement » expliquer à lui seul la sous-représentation des américains d'origine mexicaine dans les jurys de ce comté.
Intrusion des probabilités.
Lors du procès, un statisticien produisit des arguments pour convaincre la Cour Suprême du bien fondé de la requête de l'accusé (dont les juges votèrent à 5 contre 4 en faveur de la requête).
Il expliqua que le hasard ne peut pas « raisonnablement » expliquer à lui seul la sous-représentation des américains d'origine mexicaine dans les jurys de ce comté.
Quels arguments invoquer ?
Comment l'avocat peut-il espérer convaincre la cour suprême sur des critères solides?
L'angle d'attaque suivant peut-il suffire ?
On expose un schéma comme-celui ci-dessus et on crie à l'évidente discrimination, car évidence graphique?
Mais si on rétorquerait que le simple hasard peut engendrer un telle répartition:
Cette différence entre la fréquence du caractère étudié dans la population et celui dans l'échantillon, cette fluctuation d'échantillonnage peut-être elle être le fruit du hasard ou est-ce une anormalité probable?
Ainsi, pour argumenter statistiquement, on a besoin de mesurer la fluctuation d'échantillonnage.
Modélisation :
Hypothèse faite :
On sait que dans la population, la population mexicaine intervient avec une fréquence de \(p=0,791\).
Si la constitution des jurys relevait du hasard, et s'ils étaient en ce sens-là représentatifs de la population, prélever un juré ou un quelconque membre de la population et l'interroger sur son éventuelle origine mexicaine représenterait une expérience de Bernouilli dont la loi suit le même paramètre, un même taux de succès de \(p=0,791\).
Si on suppose qu'interroger successivement sur leur origine , les 870 membres indépendamment choisis des divers jurys du comté représente alors un schéma de Bernouilli, alors la variable aléatoire comptabilisant le nombre de succès suivrait la loi binomiale \(B(870 ; 0,791)\)
Exercice : A la calculatrice, donner :
Déterminer le plus petit entier \(a\) tel que \(p(X\leqslant a)>2,5\)%
Déterminer le plus petit entier \(b\) tel que \(p(X\leqslant b) \geqslant 97,5\)%
Vérifier que la probabilité que \(X\in [a ;b]\) est supérieure ou égale à 95%.
Cet intervalle contient ainsi les valeurs de X avec une probabilité de 95%.
A partir de là, donner, au risque d'erreur de 5%, un intervalle dans lequel fluctuerait la fréquence des membres du jury, dans l'hypothèse que leur constitution soit due au hasard (conformément à la modélisation ci-dessus).
