Courbes des fonctions du second degré.

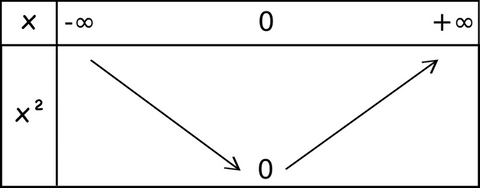
Théorème: La fonction `f`, définie sur `\mathbf{R}`, qui à `x` associe `x^2` a comme tableau de variation le précédent:

Preuve:

• Démontrons que f est croissante sur `[0 ; +\infty [ `

Soit `a` et `b` deux nombres positifs quelconques, tel que `a \le b`

On va donc vérifier que les images respectives de `a` et de `b` sont rangées dans ce même ordre:

Calculons la différence `f(a)-f(b)`:

`f(a)-f(b)=a^2-b^2`

`f(a)-f(b)=(a-b)(a+b)`

Dans ce produit, le premier facteur `a-b` est négatif ou  nul, car `a \le b`  

Le second facteur `a+b` est positif ou nul car `a` et `b` sont dans l'intervalle `[0 ; +\infty [ `

Et ainsi, `f(a)-f(b)=(a-b)(a+b)` est négatif ou nul comme produit de deux nombres de signes contraires:

`f(a)-f(b) \le 0` ce qui équivaut à dire que `f(a) \le f(b)`

On a donc `a \le b`  et `f(a) \le f(b)`: la fonction `f` conserve les inégalités: elle est donc croissante sur l'intervalle d'étude.

• Démontrer en exercice que `f`est décroissante sur `]-\infty ; 0] ` .

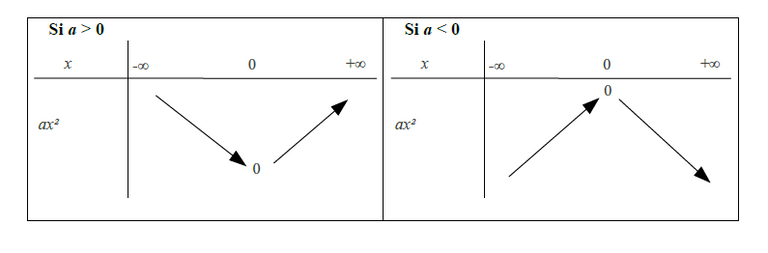
Théorème: la fonction `f_a`, définie pour tout x réel par `f_a (x)=ax^2` a les mêmes variations que la fonction carré si `a>0`, et `f_a` a des variations contraires à celle de la fonction carré si `a<0`.

Démonstration: en exercice.

Illustration graphique: Dans la figure en lien, faites varier la valeur de `a` et vérifier le théorème précédent!

Problème introductif: première question.

Théorème: (admis)

Soit une fonction `f`définie sur l'ensemble des nombres réels.

Soit `C_f` sa courbe représentative dans un repère `(O, vec(i),vec(j))`.

Soit `\alpha` un nombre fixé.

Si g est la fonction défine pour tout x réel par `g(x)=f(x-\alpha)`,

et si `C_g` est la courbe représentative de `g`, alors:

`C_g` est l'image de `C_f` par la translation horizontale de vecteur `\alpha.\vec(i)` 

Si la fonction de départ est définie par `f(x)=ax^2`, alors la courbe de `g` définie 

par `g(x)=a(x-\alpha )^2` s'obtient comme translaté horizontal de la courbe de `f`.

Exercice: expérimenter en faisant afficher la courbe de `g`et varier `\alpha` grâce au lien donné ici!

Pour finir, la courbe de la fonction `h` définie par : `h(x)=a(x- \alpha )^2 +\beta`

s'obtient par comme image par la translation verticale de vecteur `\beta.\vec(j)` de la courbe de `g`.

Illustration geogebra ici! : faites afficher la courbe de `h`et varier la valeur de `\alpha et \beta`.

En conclusion, si l'on part de la courbe de la fonction `ax^2`, parabole de sommet (0 ; 0),

la translation horizontale de vecteur `\alpha.\vec(i)`  donne la courbe de `a(x-\alpha )^2`.

A partir de cette dernière, une translation verticale de vecteur `\beta.\vec(j)` donne alors 

la courbe de `a(x- \alpha )^2 +\beta`:

cette dernière est donc une parabole de sommet `(\alpha ,\beta )`.

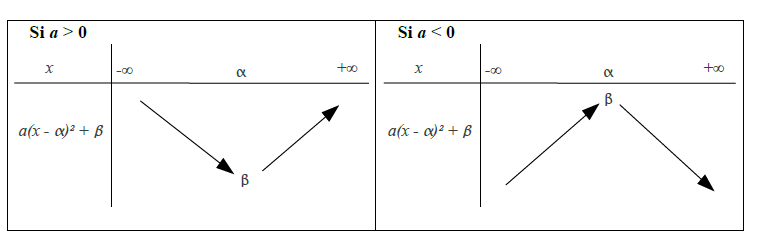
On en déduit le tableau de variation des fonctions `a(x-\alpha )^2 +\beta`:

Exercice: Répondre au problème introductif.

Exercice interactif: Le tueur du second degré.
Donner du trinôme les racines éventuelles, préciser la forme de la courbe, la nature de son extremum:
donner le tableau de variation.

Exercice Python ici: (cliquer sur "fork this" et modifier le programme)
Expliquer pourquoi le programme ci-dessous est incomplet, et le terminer!
Il devra, le cas échéant, du polynôme donné par ses coefficients a, b, et c, en donner les racines.