II-0pérations sur les événements .
Lorsqu'en primaire, on calcule l'aire d'une figure, en la décomposant en figures élémentaires disjointes, on commence déjà implicitement à entrevoir le mode d'action de cette mesure de surface. La probabilité qui par essence même mesure les ensembles, opérera de la même manière. On a donc besoin de définir quelques opérations élémentaires sur
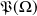, l'ensemble de événements.
On considère un sous-ensemble
d'un ensemble
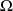, un événement, donc, de l'univers
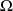. L'ensemble des éléments de l'univers qui ne sont pas dans
s'appelle le complémentaire de
dans
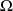, et en probabilité, on l'appellera événement contraire de
, et on le notera:
).
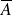On considère deux sous-ensembles(ou parties)
et
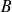d'un ensemble
.
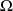(en probabilité, on dira plutôt deux événements de l'univers
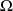). On appelle intersection de ces événements, et on note
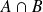leur partie commune, ensemble des éléments de
et simultanément de
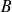( événement “
et
”).
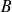On appelle union de ces événements et on note
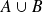l'ensemble des éléments appartenant indifféremment à
ou à
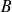(événement “
ou
”).
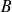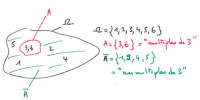
Dans l'exemple ci-contre,
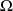est l'univers du lancer de dé,
est l'événement "Issues paires",
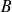est l'événement "Issues multiples de 3". Les événements
et
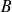sont compatibles, d'intersection {6}. L'événement contraire à leur réunion est {1, 5}. Ceux des issues qui n’appartiennent pas à
ou B, qui ne sont donc ni dans
, ni dans
.
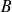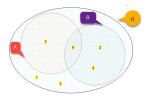
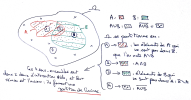
Dans un cas plus général, deux événements A et B partitionnent l'univers en 4 sous-ensembles , conformément à la patate ci-dessous :
Les démonstrations des formules ensemblistes du type
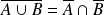en deviennent triviales.
si
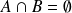, si la partie commune est vide, on dit que ces sous-ensembles
et
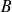sont disjoints (que les événements
et
sont incompatibles).
