III-Probabilités sur l'univers
Notre univers étant défini, à tout événement de l'univers, on associe alors un nombre positif qui permet de quantifier son degré de vraisemblance
(0 étant l'invraisemblable, 1 exprimant la quasi-certitude), ce nombre devant par ailleurs répondre à tout ce que l'on attend intuitivement d'une probabilité:
Une probabilité est une fonction de l'ensemble des événements de
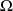vers l'intervalle [0;1]:
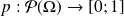
La probabilité d'être dans l'univers est de 100%:
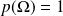
si
et
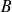sont deux événements disjoints, incompatibles, alors
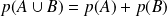
(Ici,
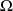est fini, sinon cet axiome mérite des adaptations)
La probabilité de la réunion de deux sous-ensembles disjoints est la somme des probabilités de ces événements.
Et cette propriété se généralise par itération à une réunion quelconque d'ensembles disjoints... On est sur un univers fini.
Conséquences immédiates:
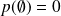.En effet comme
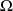et
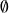sont des ensembles disjoints, et que leur union est l'univers, (ce sont des événements contraires):
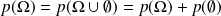, et ainsi: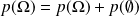
D'où le résultat.
Si
et
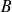sont deux événements contraires, donc d'union l'univers et d'intersection vide, alors
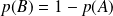.Preuve: s'inspirer de la précédente!
Pour tout événement
constitués des issues en nombre fini (événements élémentaires) a, b, c...z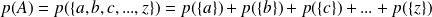
Si on considère deux événements quelconques
et
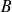, non nécessairement disjoints,
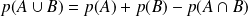
En effet, les ensembles
et
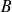partitionnent l'univers en quatre parties disjointes deux à deux comme précisé dans la figure ci-dessous, et le résultat en découle aisément.
Exemple d'univers probabilisé: Dans le lancer du dé équilibré à six faces, si on attribue à chaque issue la même probabilité (chaque face est équiprobable, ce que l'énoncé nous invite à croire en parlant de dé équilibré):
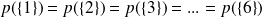. Appelons p cette probabilité commune: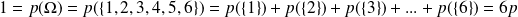
D'où:
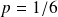
Si l'on s'intéresse à l'événement A=“obtenir un nombre pair”, c'est à dire le sous-ensemble de l'univers :
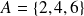, sa probabilité est de :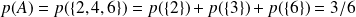
En généralisant ce calcul à d'autres événements, dans le cas de l'équiprobabilité, la probabilité s'obtient aisément par la formule:
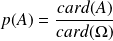où
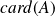désigne le nombre d'éléments de l'événement
.(son cardinal dit-on).soit en pratique:
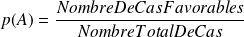
Le dé aurait été truqué, c'est une autre probabilité que l'on aurait fait agir, et qui modéliserait bien mieux le dispositif expérimental.
Par exemple, disons que l'on dispose d'un dé cubique, pipé de telle sorte que la probabilité d'apparition du 6 soit sept fois plus importante que celle des autres faces, elles équiprobables. Ici, le même univers serait muni d'une probabilité cohérente avec le trucage effectué, appelons la p' :
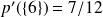et
