Coefficients binomiaux.
Les "k parmi n" introduits précédemment s'appellent des coefficients binomiaux.
\(\binom{n}{k}\) est par définition le nombre de chemins comportant exactement k succès dans un schéma de bernouilli à \(n\) répétitions.
On peut l'appréhender de diverses manières :
Il s'agit également du nombre de mots à \(n\) lettres ne comportant que des S ou des E, et comportant exactement \(k\) lettres S.
Il s'agit du nombre de parties à \(k\) éléments d'un ensemble qui en comporte \(n\).
Nous allons comprendre comment on peut générer un protocole qui nous donne l'accés à la valeur de \(\binom{n}{k}\) pour \(n\) et \(k\) donnés entiers naturels.
Fondamental : Quelques premiers résultats sur les coefficients binomiaux.
Soit un entier naturel \(n\) strictement positif, soit k un entier naturel qui lui est inférieur ou égal.
\(\binom{n}{0}=1\): en effet, ceci correspond au nombre de chemin sur le schéma de Bernouilli à \(n\) répétitions ne comportant aucun succès : il n'existe qu'un seul tel chemin : celui qui amène l'échec à chaque répétition. ( circuit du serial looser).
Un autre manière d'appréhender cette égalité est de se souvenir que le seul moyen de choisir \(0\) éléments dans un ensemble à \(n\) éléments, est de ne choisir personne !
PS : on admet que \(\binom{0}{0}=1\).
\(\binom{n}{n}=1\): en effet, ceci correspond au nombre de chemin sur le schéma de Bernouilli à \(n\) répétitions ne comportant que des succès :il n'existe qu'un seul tel chemin : celui qui amène le succès à chaque répétition. ( circuit du serial winner).
Un autre manière d'appréhender cette égalité est de se souvenir que le seul moyen de choisir \(n\) éléments dans un ensemble à \(n\) éléments, est de tous les choisir !
\(\binom{n}{k}=\binom{n-k}{k}\) . En effet, choisir \(k\) personnes parmi \(n\) et décider de les enfermer, c'est exactement choisir les \(n-k\) autres auquel on laisse la liberté. Et sur le schéma de Bernouilli à \(n\) répétitions, tout chemin comportant exactement \(k\) succès comporte exactement \(n-k\) échecs et vice-versa : dénombrer les uns revient à dénombrer les autres.
\(\binom{n}{1}=n\): en effet, choisir une seule personne dans un ensemble à \(n\) éléments offre \(n\) possibilités différentes.
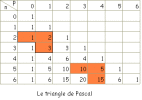
Fondamental : Formule du triangle de Pascal
Il est urgent de pouvoir accéder aux \(\binom{n}{k}\) autrement qu'en énumérant des chemins ou des sous-ensembles...
Sur un schéma de Benouilli à \(n+1\) répétitions, on désire dénombrer les chemins comportant exactement \(k+1\) succès :
on cherche donc \(\binom{n+1}{k+1}\) .
Or sur un tel schéma, pour tout chemin considéré :
De deux choses l'une :
Ou bien il commence par un succès, auquel cas dans la suite de l'arbre qui est celui d'un schéma de Bernouilli à \(n\) répétitions, il faudra dénombrer les chemins comportant encore \(k\) succès exactement. Ce qui n'est rien d'autre que \(\binom{n}{k}\) .
Ou bien il commence commence par un échec, auquel cas dans la suite de l'arbre qui est celui d'un schéma de Bernouilli à \(n\) répétitions, il faudra dénombrer les chemins comportant encore \(k+1\) succès exactement. Ce qui n'est rien d'autre que \(\binom{n}{k+1}\) .
Ainsi, nous obtenons la formule suivante :
\(\binom{n+1}{k+1}\)= \(\binom{n}{k}\)+ \(\binom{n}{k+1}\)
Dès lors, si on construit un tableau \(n\times k\), cette formule couplée avec les résultats du paragraphe précédent, nous permet de calculer les combinaisons de proche en proche dans le tableau.
En effet, les combinaisons sont ainsi placées dans le tableau :
k | k+1 | |
|---|---|---|
n | \(\binom{n}{k}\) | \(\binom{n}{k+1}\) |
n+1 | \(\binom{n+1}{k+1}\) |
Et on applique la formule du triangle de Pascal qui dit que la somme de deux cellules adjacentes et sur une même ligne donne celle en dessous de la cellule la plus à droite.
Complément : Autre technique de génération des combinaisons : hors-programme.
Exemple : Dans un classe de 32 élèves, on veut choisir un bureau de 5 personnes, et 1 président distincts des membres du bureau.
Combien de possibilités ?
Pour effectivement un tel choix, on peut opter pour deux protocoles différents :
On commence à choisir 6 personnes, soit \(\binom{32}{6}\) possibilités, et parmi elles, on choisit le président (6 possibilités par bureau choisi):
On dénombre ainsi \(\binom{32}{6} \times 6\) possibilités en tout.
Ou sinon, on commence par choisir le président dans la classe ( 32 possibilités), puis on choisit les 5 membres du bureau dans le reste de la classe, soit \(\binom{31}{5}\) possibilités par président choisi.
On dénombre ainsi \(\binom{31}{5} \times 32\) possibilités en tout.
Ainsi, on obtient :
\(\binom{32}{6} \times 6 = \binom{31}{5} \times 32\)
Soit
\(\binom{32}{6} = \binom{31}{5} \times \frac{32}{6}\)
En réitérant le processus, on montre que :
\(\binom{31}{5} = \binom{30}{4} \times \frac{31}{5} \)
\(\binom{30}{4} = \binom{29}{3} \times \frac{30}{3} \)
\(\binom{29}{3} = \binom{28}{2} \times \frac{29}{2} \)
\(\binom{28}{2} = \binom{27}{1} \times \frac{28}{1} \)
Or nous savons que \(\binom{27}{1}=27 \)
Et ainsi :
\(\binom{32}{6}= \frac{32}{6} \times \frac{31}{5} \times \frac{29}{4} \times \frac{28}{3} \times \frac{29}{2} \times \frac{28}{1}\times 27 \) \(\) \((*)\)
Définition : Soit n un entier naturel, on appelle factorielle de \(n\), et on note \(n!\) :
le nombre 1 si n est nul :\( 0!=1\)
le produit des entiers naturels non nuls qui précèdent n sinon : \(n != n\times (n-1) \times (n-2) ...\times 2 \times 1.\)
Ainsi, avec cette définition, on reconnaît au numérateur de l'expression de \(\binom{32}{6}\) donné par \((*)\) le rapport \(\frac{32!}{28!}\)
Quant au dénominateur, il s'y trouve \(6!\)
On obtient \(\binom{32}{6}=\frac{32!}{6!\times 28 !}\)
En généralisant immédiatement le procédé ci-dessus, on obtient :
\(\binom{n}{k}=\frac{n!}{k!\times (n-k)!}\)