Expérience et schéma de Bernouilli

Si on suppose que dans la population, le jour de naissance est de manière équiprobable lundi, mardi...dimanche, donc d'une probabilité p=1/7.

On interroge un membre de l'équipe gagnante :

S'il est né le bon jour, on parle de succès, sinon d'échec. La probabilité du succès est de 1/7. On réalise ainsi à chaque interrogatoire, une expérience de Bernouilli.

On répète cette expérience à chacun des autres membres de l'équipe.

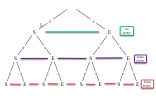
Cette répétition indépendante et identique de l'expérience de Bernouilli dessine ce que par définition, on appelle un schéma de Bernouilli, qui se visualise par l'arbre de probabilité suivant :

^[1]

L'univers initial peut ainsi se modéliser par les mots de trois lettres formés des lettres S et E.

SSS, SSE, SES, SEE, etc. Où par exemple SES correspond à l'issue " Le premier joueur est né le bon jour, pas le second mais le troisième si.".

Il est pertinent dans cet exercice de s'intéresser à la variable aléatoire \(X\) qui compte le nombre de succès de chaque issue, le nombre de S dans chaque mot représentant une issue.

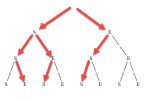
Ainsi l’événement "deux joueurs de l'équipe sont nés le bon jour", à savoir " \(X=2\) "se visualise par les trois chemins suivants de l'arbre de probabilité :

La lecture des probabilités par produit sur le chemin donne pour chaque issue de cet événement "deux joueurs de l'équipe sont nés le bon jour" :

\(p(SSE)= p \times p \times q\), à savoir :\(p^2q\)

\(p(SES)= p \times q \times p \times q\) à savoir...\(p^2q\).

\(p(ESS)= p \times q \times p\), à savoir :\(p^2q\) à savoir encore \(p^2q\)

Ainsi ce \(p^2q\) intervient trois fois, soit autant que de chemins vérifiant la condition : il y a trois chemins répondant au critère.

On conclut que : \(p(X=2)=3p^2q\).

Dans cette probabilité, L'exposant 2 de \(p\) est le nombre de succès désirés. Celui de \(q\) (ici 1) est le nombre d'échec conséquent.

Quand au nombre entier naturel 3, il correspond au nombre de chemins de l'arbre comportant deux succès sur les trois branches du trajet :

ce nombre se notera \(\binom{3}{2}\), et se lira " 2 parmi 3 " ;

Si évidemment ici, il s'agit de 3, cette définition s'imposera dès qu'il faudra généraliser le schéma de Bernoulli avec un nombre de répétitions plus conséquent.

Définition : On appelera " k parmi n", et on notera \(\binom{n}{k}\) le nombre de chemins comportant k succès sur un schéma de Bernoulli à n répétitions.

Si \(X\) est la variable aléatoire comptabilisant le nombres de succès, \(X\) prend toutes les valeurs entières entre 0 et 3.

Et nous pouvons donner la loi de probabilité de \(X\) en raisonnant comme précédemment :

Ce qui se réécrit avec les notations développées dans l'indice précédent :

La somme des exposants de \(p\) et de \(q\) est pour chaque issue de 3, ce qui correspond au nombre de répétition, au nombre de branches des chemins de l'arbre.