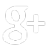Vers la formalisation numérique, acte II

Sur la courbe de la fonction y=f(x), on se place au voisinage d'un point A fixé de cette courbe, d'abscisse a et d'ordonnée f(a).

Soit M un point de la courbe, proche de A. Son abscisse prend la forme a+h, et son ordonnée est donc f(a+h):

M distinct de A, le coefficient directeur de la sécante est:

`a_{h}=\frac{f(a+h)-f(a)}{h},h \ne 0 `

MLe rapport précédent s'appelle taux d'accroissement en a de la fonction `f`.

De même que l'on rapproche géométriquement le point `M` du point `A`, de même dans les calculs, on fait donc tendre `h` vers O:
Le coefficient directeur de la sécante `(AM)` s'approchera alors de celui de la sécante à la courbe en `A`.
`a_{h}=\frac{f(a+h)-f(a)}{h},h \ne 0 `

Si ce nombre limite existe, on l'appelera alors nombre dérivé de `f` en `a` et on le notera `f'(a)`
`a_{h}=\frac{f(a+h)-f(a)}{h},h \ne 0 `

Dans le calcul précédent du taux d'accroissement, pour toutes les fonctions usuelles, on remarquera une disparition étrange de `h` au dénominateur:
quand on amène alors `h` vers 0, cela ne génère pas ainsi une "division par zéro"...
Exemple: pour `f(x)=x^{2}` au point `A` d'abscisse `a`, pour ` h \ne 0 ` :

`a_{h}=\frac{f(a+h)-f(a)}{h},h \ne 0 `

`a_{h}=\frac{(a+h)^{2}-a^2}{h}`

`a_{h}=\frac{a^2+2ah+h^{2}-a^2}{h}`

`a_{h}=\frac{2ah+h^{2}}{h}`

`a_{h}= 2a+h`

Ainsi, si `h \rightarrow 0`, alors `a_{h}\rightarrow 2a` :

Le coefficient directeur de la tangente au point `A` d'abscisse `a` est `2a`. On écrit: `f'(a)= 2a`.
Exemple:
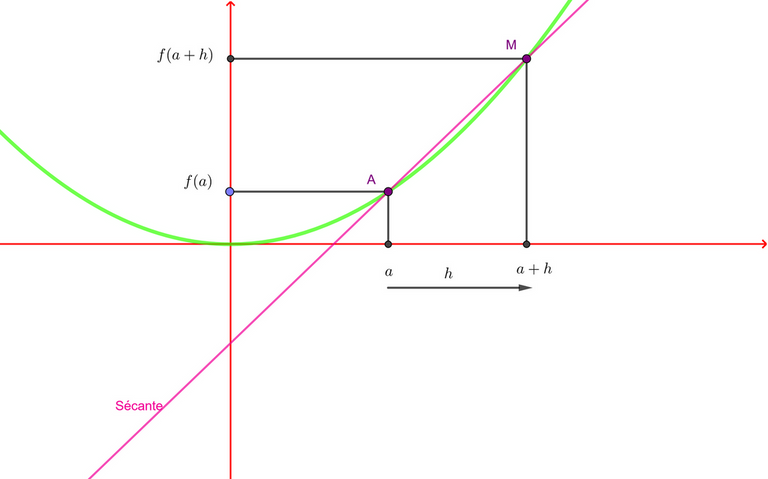
Si `a=1`, on a `f'(1)= 2`: le coefficient directeur de la tangente à la parabole `y=x^2` est de 2.
De cette tangente, on connait ainsi le point A, et le coefficient directeur. On la connait donc intégralement.